Image
Quantum Computing
The goal of this course is to introduce the main concepts and challenges of quantum computing, a new set of technologies and techniques that promise to solve hard computational problems.
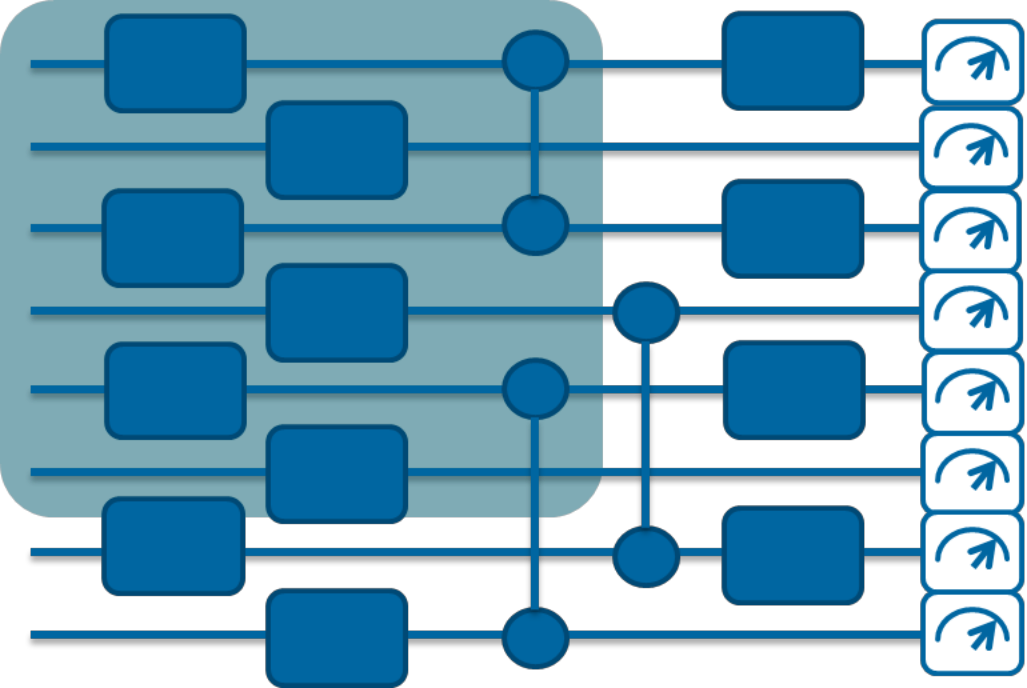
We will review both the theoretical premises and promises of ideal quantum computers, and the practical challenges that one faces when one actually runs quantum programs on today’s physical quantum computers: what is the role of decoherence? how does one deal with it in practical quantum algorithms?
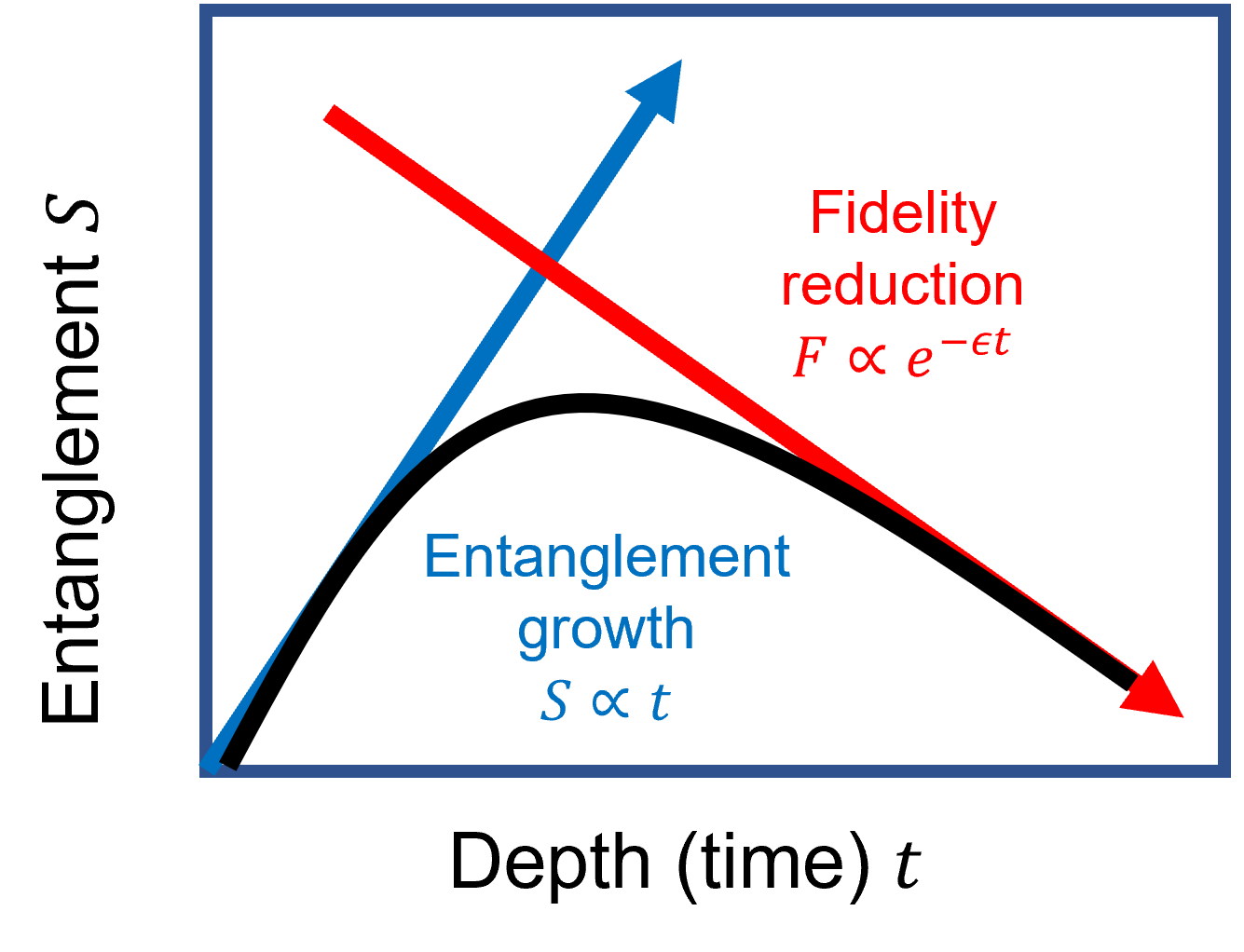
The course will also introduce the key concepts of quantum error correction, which could be used when sufficient qubit counts and qualities are reached.
The course will combine conventional blackboard lectures and exercise sessions with small quantum programming numerical projects and short research journal clubs.
Syllabus
A. Quantum computing in theory
- quantum computing through the tensor network lens
- entanglement (and more tensor networks)
- quantum computing for fermionic problems
B. Quantum computing in practice
- noise and decoherence in quantum computers
- variational quantum algorithms: promises and challenges
- overcoming VQE challenges
- analog quantum computing
C. Long-term quantum computing
- advanced Hamiltonian simulation algorithms
- quantum error correction 101.
Prerequisites
Standard linear algebra. Quantum mechanics.
Basic quantum algorithmics is supposed to be known: quantum gates and circuits.
Evaluation
Written exam & article presentation.